Abstrict

Pharmacokinetic models utilize mathematical terms to do pharmacokinetic analysis. Pharmacokinetic analysis of drug is defined as an experimental method to find drug exposure once administered or how does drug behave inside the body. Pharmacokinetic parameters determined include drug absorption, distribution, metabolism and elimination after its administration. These two types of models are used compartment and non -compartment models. A compartment is defined as space inside the body that a drug occupies upon its administration. When there is linear kinetics, it is desirable to use a simple non-compartment model with lesser assumptions, while when a compound follows non-linear kinetic, it is preferred to use a compartment model. Non- compartment model utilizes concentration-time data to predict C max, t max, AUC and AUMC for the administered compound. AUC and AUMC can be calculated using the trapezoidal rule. Pharmacokinetic parameters can also be predicted using statistical moment theory.

Keywords

Compartment, Non -compartment Model, AUC, AUMC, MRT, Drug.

Introduction

Mathematical Model

Mathematical model explains the biological systems in mathematical terms and also provides quantitative relationships. Model is defined as one that describes the quantitative relationships using mathematical explanation. (Banwarth-Kuhn & Sindi, 2020). A collection of mathematical operation, quantities and relations together with the definitions are known as mathematical models; they must employ a realistic and practical approach.




Pharmacokinetic Model

Pharmacokinetic compartment is defined as the space where the drug resides in the body, and it is not required for the compartment to be corresponding with any anatomical space or physiological volume. In this model, changes in drug concentration with respect to time are evaluated. A concept that explains quantitative relationships in mathematical terms are known as the pharmacokinetic model. (Moreno-Vargas, & Prada-Gracia, 2016).




Compartment Model

A compartment is defined as a group of tissues that share the same blood flow and have the same drug affinity that corresponds to the anatomical space or physiologic volume. The compartment model is the oldest approach and widely used model for pharmacokinetic analysis. (Nagayasu, Ozeki &  Onoue, 2019). It utilizes experimental data to predict the concentration of a drug with respect to time by using quantitative formulas. It is applicable to non-linear and linear pharmacokinetics.




Non-Compartment Model

Non-compartment model is the model-independent that does not require the assumption of a specific model for the drug or its metabolite. The only restriction associated with the non-compartment model is that the drug or its metabolite must follow linear kinetics. Without assuming any compartment model, it is useful to study the time course of the drug or pharmacokinetic parameters of the drug in the body. It overcomes the drawbacks which are associated with other models. It basically assumes that the metabolites follow first-order kinetics. Non-compartment allows the detailed pharmacokinetic analysis without using any sophisticated computer or curve fitting or any mathematical formulas. This model has widely used for solving many problems and used for clinical application in pharmacokinetics but no all-pharmacokinetic problems.




The Non-Compartmental Analysis

Non-compartmental analyses provide an alternative method for describing drug pharmacokinetics without having to assign a particular compartmental model to the drug. Although this method is often considered to be model-independent, there are still a few assumptions and key considerations that must not be overlooked. This approach is, therefore, better referred to as “non-compartmental” as it does assume a “model” in that, among other things that will be reviewed below, the PK needs to be linear, and the terminal phase must be log linear. (Wang, Z. et al., 2010).

The first supposition is that linear pharmacokinetics is displayed by the drug in question, or we can say that exposure increases in proportion with increasing dose and PK parameters are stable in the course of time. A second significant assumption is that the elimination of the drug from the body strictly from the pool in which it is being measured, for example, the plasma. All sources of the drug are direct and unique to the measured pool is the final supposition of this approach. . (Park & Kim, 2019).

Anticipated plasma concentration profile is the significant measure that describes the life of the drug in the body after extravascular or intravenous administration. AUC can be computed by using linear or log trapezoidal rule or their combination. (Acharya, C. et al., 2016)

AUC for two adjacent points, t1 and t2, can be calculated by using the linear trapezoidal rule on linear scales through the mathematical equation given below.

AUCt₁-t₂ =

Where AUCt1-t2 is an area of trapezoid between t1 and t2.




The Following Equation is used by the Log Trapezoidal Method

AUCt₁-t₂ =




Trapezoidal rule is the most reliable rule for computing data of ascending and declining curve, but there are higher chances of error if the concerned curve is sharp bending. Log trapezoidal rule is generally considered the most reliable method of computing exponentially declining curves but cannot be employed for ascending curve as there is a high chance of unavoidable error. There is software available like Phoenix1 WinNonlin1, Certera where a combination of linear and log trapezoidal rule can be employed. (Jawie?, W. et al., 2013).

Statistical Moment Theory-Based Non-Compartment Analysis

Statistical Moment Theory

It is defined as the numerical explanation of discrete distribution data that is calculated by collecting concentration-time data that represents the true moment or the true probability density function (PDF) estimation which shows the true relationship between time and concentration. (Cai, D & Tao, L, 2011).




Explanation

Non-compartment analysis is based on statistical moment theory, where experimental data is collected following single-dose administration. Statistical moment theory allows to study time-related changes in such events that are resulted from constitutive elements. Ng Non compartment analysis can be applied to any model if the pharmacokinetics given is the liner. It does not require to suppose one specific model for a drug or its metabolite. Statistical distribution or moment curve shows the time concentration of drug in the blood plasma, which is generally represented by equation 1.

µm or mth moment =?_0^??0tmf(t). dt --------Equation 1

where probability density function is represented by f(t), time by t and m is the mth moment.

Irrespective of the routes of administration, the first two statistical moments are as follows:

When m=0, substituting m=0, then equation 1 will become

µo=?_0^??0f(t). dt

where µo is called as zero moment

Similarly, substituting m=1 in equation 1, then the first moment will be given as

µ1 =?_0^??0t1f(t). dt

The mean of the distribution is defined by the first moment.

When statistical distribution or moment curve shows the time course of drug concentration in blood plasma, then the equation used to calculate this time course will be given as, 

MRT = AUMC/AUC 

Where in the above equation,

MRT stands for mean residence time, which represents the average time a drug stayed in the body. 

AUMC stands for the area under the first moment curve that is given by ?_0^??0C(t).dt. AUMC can be calculated by plotting a graph between the product of plasma drug concentration and time on the y-axis and time from zero to infinity on the x-axis. (Shebley, M et al., 2018)

AUC stands for the area under the zero-moment curve that is given by ?_0^??0C.dt. AUC can be obtained by plotting a graph between plasma drug concentration on the y-axis and time from zero to infinity on the y-axis. (Dei Cas, M & Ghidoni, 2019)  

AUC and AUMC can also be calculated by finding moments through numerical integration utilizing trapezoidal rule from the data of concentration of drug and time following administration of the drug. But this method has only been used to find zero and the first moment in the pharmacokinetic analysis as the chances of unacceptable computational error increases with the higher moments.




Formula given for Calculating Area of Trapezoidal = 1\2 (Cn-1+ Cn) (tn – tn-1)

While Area under the curve = ? (Area of trapezoids)

 




Estimating AUC &  AUMC




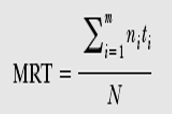
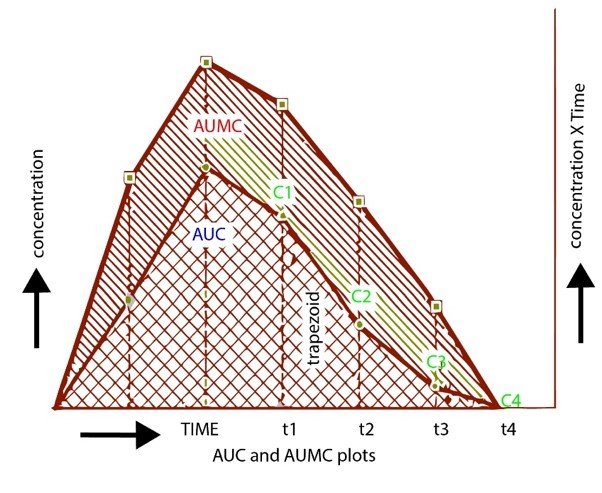
For Samples until the Last Observed Concentration 

AUC t1-t2 = (t1-t2). (C1+C2)/2

AUMC t1-t2 = (t1-t2). (t1.C1) +(t2.C2) / 2

And when t2=t inf then, 

AUC t last- t inf = Clast / ?

AUMC t last - t inf = t last. C last / ? + C last / ?2




Where, 

Clast = last concentration at time t last  

? = Slope of termination phase of a concentration-time profile when graph plotted between the log of concentration versus time (semi-log graph)




Limitation of Statistical Moment Theory 

Despite its application in a wide range of analysis, particularly in the characterization of the pharmacokinetics of the drug, it has some limitations

Statistical moment theory can not be employed for the non-linear event.

It does not give sufficient information about the time course of the drug in the body; therefore. Usually, mean values are employed.




Mean Residence Time

Mean residence time is defined as the time which is spent by the drug prior to its elimination from the body.

 MRT= Drug(total) residence time in the body

Total number of drug molecules

MRT= AUMC = ? tx C. dt

AUC         ? C. dt

When IV bolus injection is administered, the time required for 63.2% of the drug to be eliminated is known as MRT. After IV bolus injection, the calculation of MRT determines the elimination of the drug from the body. The plasma elimination half-life, i.e., t1/2, is similar to MRT. Both distribution and elimination are the functions of MRT as in the case of half-life.(Ki S, 2020).

In IV bolus   MRT= 1/k10

In non-compartmental terms, MRT =  1/k

Vss is the volume of distribution at a steady state.

The clearance ration to Vss is referred to as K, which is constant.

 t  1/2  , which is termed as Plasma elimination half-life = 0.693/(k 10)                               

  t1/2=0.693MRT

MRT is used for the comparison, e.g.:

Constant rate of infusion: MRTiv=MRTinst - T/2

Where T is the duration of infusion




Drug Absorption

A pharmacokinetic parameter by which drug is absorbed from the dosage form into the blood. The factors which affect the drug absorption in the body include the route of administration and formulation of the drug.

The pharmacokinetic parameters include bioavailability and absorption rate constant.

            Mean absorption time is the difference in the mean residence time after different modes of administration.

MAT = MRTni – MRTiv

By non-instantaneous route, h, the mean residence time of the drug is represented by MRTni.

By intravenous bolus injection. The mean residence time of the drug is represented by MRTiv.

For IM injection, this equation is also used.

MAT = 1/ka




Absorption half-life can be given by t1/2 = 0.693/ka

Absorption half-life, t1/2 = 0.693MAT

When zero-order is followed by absorption then,

MAT = T/2

Where absorption occurs at time T

To compare different dosage forms, MAT can be used.




Other Parrameters Of Mrt

Mean dissolution time, i.e., MDT, is represented by

MDT= MRTtest- MRTsoln

For oral administration,

MRToral = MRTiv + 1/Ka

To evaluate data for absorption analysis,

MAT = MRTtest - MRTiv

MAT = 1/Ka

 The first order absorption rate constant is given by Ka.

Pharmacokinetic Parameters in Non-Compartment Model

Drug Clearance

Drug clearance is defined as the removal of the drug from the plasma over a specified period of time. (Mahmoud, S. H & Shen, 2017)

After the intravenous administration of the drug, it either accumulates in the blood plasma or redistributes into the tissues. The volume of plasma cleared of the drug is through the renal or hepatic clearance. (Horde, G. W & Gupta, 2021).

It plays a very important role in calculating the dose of the drug and dosing regimens for the patients. It is measured in the units of volume/time. (Atkinson A. J, 2018).

After IV bolus administration, 

Cl = Dose iv/AUC

At steady state after constant rate intravenous infusion 

Cl = ko / Css

Where ko is the rate of infusion and steady state concentration is given by Css. 

The extraction ratio >> Cl=Q(ER) to be applied in this case.




Apparent Volume of Distribution

After oral or parenteral administration, the drug is uniformly distributed between plasma or the rest of the body tissues and this term is known as apparent volume of distribution. It is useful for predicting the amount of drug in the body.

The volume of distribution at steady-state independent of elimination is given by Vss.

Vss =i. v dose (AUMC) / (AUC)

If the drug is given by constant rate intravenous infusion 

Vss = infused dose (AUMC) / (AUC)2 – infused dose * ? / 2(AUC)

Vss = k0 * ? (AUMC)/2(AUC)2 – k0 ?2 / 2(AUC)

Where the rate of infusion is given by ko and ? is the duration of infusion




Steady State Plasma Drug Concentration

The total body clearance of the drug in a patient, and

the effective rate of drug dosing is termed as Css. (Wadhwa, R. R & Cascella, M, 2020)

In continuous infusion 

Css = k0 /Cl

In multiple dosage regimen 

C = AUCss / ?




At a steady state, the average plasma drug concentration is given by C.




Predicting the Time to Steady State

? Time required by the drug to reach a steady state, i.e., 99%, which takes 6.65 half-lives.

? The time required to reach ss in case of the extravascular route is greater than estimated by biological half-life.

? The time required to attain ss in case of multicompartment disposition is shorter than that estimated by terminal half-life.

fss =AUC0t/AUC

In case noncompartmental models, when the drug is administered repetitive or recurring dosing, fss.

The area under the curve in a single dose is termed as AUC.




Bioavailability

Bioavailability can be defined as the amount of drug that reaches systemic circulation.

Bioavailability is referred to as unity (=1) in the case of Iv injection. It ranges from 0 to 1.

Bioavailability (F) of a dosage form can be given as

Absolute bioavailability, F = AUC oral Div / AUC IV Doral

In absolute bioavailability, the oral dose is considered as the reference standard, whereas, in relative bioavailability, other dosage forms can be considered as reference.

Relative bioavailability, Fr may be expressed by comparing the zero moments of a product with a standard product.

Relative bioavailability Frel = (AUC) drug / (AUC) standard

Bioavailability studies are significant for the low therapeutic drugs, sustained release of the drug formulation and drugs which undergoes first-pass metabolism.




Fraction Metabolized

Fraction metabolized can be given by the formula.

Fm = AUC x1/ AUC1

? Area under the curve of metabolite concentration in plasma in opposition to time from zero to infinity is termed as AUCx1.

? The total area under the metabolite concentration –time curve after an equimolar intravenous dose of a metabolite is termed as AUC1.

Conclusion

Pharmacokinetic analysis has prime importance in the development of new drug. It is defined as an experimental method, used to determine drug behavior in the body once administered or what does body do to the drug. The pharmacokinetic analysis enables us to find drug exposure, including its absorption, metabolism, distribution and excretion. There are two most widely used methods available to determine the pharmacokinetics of drug, i.e., compartment model and non -compartment model. A compartment is defined as the space occupied by a drug inside the body. Non-compartment model overcomes the limitations associated with the compartment model. That is, it does not require a specific model to find pharmacokinetics and quantitative relationship. But there are few limitations associated with non-compartment analysis. It is used for drugs that follow non-linear kinetics. Trapezoidal rule and statistical moment theory can be used in non- compartment analysis to find certain parameters like mean residence time, AUC (area under the curve), Cmax, t max, fraction metabolized fm and bioavailability through concentration-time profile.

References

• Nagayasu, M., Ozeki, K., & Onoue, S. (2019). Three- Compartment Model Analysis with Minimal Sampling Points in the Caco-2 Permeability Assay. Biological & pharmaceutical bulletin, 42(9), 1600-1604. https://doi.org/10.1248/bpb.b19-00221
• Wang, Z., Kim, S., Quinney, S. K., Zhou, J., & Li, L. (2010). Non-compartment model to compartment model pharmacokinetics transformation meta-analysis--a multivariate non-linear mixed model. BMC systems biology, 4 Suppl 1(Suppl 1), S8. https://doi.org/10.1186/1752-0509-4-S1-S8
• 3.Park, J. S., & Kim, J. R. (2019). Non-compartmental data analysis using SimBiology and MATLAB. Translational and clinical pharmacology, 27(3), 89-91. https://doi.org/10.12793/tcp.2019.27.3.89
• Acharya, C., Hooker, A. C., Türkyılmaz, G. Y., Jönsson, S., & Karlsson, M. O. (2016). A diagnostic tool for population models using non-compartmental analysis: The ncappc package for R. Computer methods and programs in biomedicine, 127, 83-93. https://doi.org/10.1016/j.cmpb.2016.01.013
• Jawień, W., Majcherczyk, J., Kulza, M., Florek, E., & Piekoszewski, W. (2013). How to combine non- compartmental analysis with the population pharmacokinetics? A study of tobacco smoke's influence on the bioavailability of racemic citalopram in rats. Pharmacological reports : PR, 65(2), 517-524. https://doi.org/10.1016/s1734-1140(13)71028- 4
• Cai, D., & Tao, L. (2011). Statistical physics approaches to neuronal network dynamics. Sheng li xue bao : [Acta physiologica Sinica], 63(5), 453-462.
• Dei Cas, M., & Ghidoni, R. (2019). Dietary Curcumin: Correlation between Bioavailability and Health Potential. Nutrients, 11(9), 2147. https://doi.org/10.3390/nu11092147
• Horde, G. W., & Gupta, V. (2021). Drug Clearance. In StatPearls. StatPearls Publishing
• Mahmoud, S. H., & Shen, C. (2017). Augmented Renal Clearance in Critical Illness: An Important Consideration in Drug Dosing. Pharmaceutics, 9(3), 36. https://doi.org/10.3390/pharmaceutics90300 36
• Atkinson A. J., Jr (2018). Augmented renal clearance. Translational and clinical pharmacology, 26(3), 111-114. https://doi.org/10.12793/tcp.2018.26.3.111
• Wadhwa, R. R., & Cascella, M. (2020). Steady State Concentration. In StatPearls. StatPearls Publishing.
• Ki S. (2020). A semi-compartmental model describing the pharmacokinetic- pharmacodynamic relationship. Anesthesia and pain medicine, 15(1), 1-7. https://doi.org/10.17085/apm.2020.15.1.1
• Shebley, M., Sandhu, P., Emami Riedmaier, A., Jamei, M., Narayanan, R., Patel, A., Peters, S. A., Reddy, V. P., Zheng, M., de Zwart, L., Beneton, M., Bouzom, F., Chen, J., Chen, Y., Cleary, Y., Collins, C., Dickinson, G. L., Djebli, N., Einolf, H. J., Gardner, I., ... Rowland, M. (2018). Physiologically Based Pharmacokinetic Model Qualification and Reporting Procedures for Regulatory Submissions: A Consortium Perspective. Clinical pharmacology and therapeutics, 104(1), 88-11 https://doi.org/10.1002/cpt.1013
• Banwarth-Kuhn, M., & Sindi, S. (2020). How and why to build a mathematical model: A case study using prion aggregation. The Journal of biological chemistry, 295(15), 5022-5035. https://doi.org/10.1074/jbc.REV119.009851
• Moreno-Vargas, L. M., & Prada-Gracia, D. (2016). New perspectives on the computational characterization of the kinetics of binding- unbinding in drug design: implications for novel therapies. Boletin medico del Hospital Infantil de Mexico, 73(6), 424-431. https://doi.org/10.1016/j.bmhimx.2016.11.003